Nicolò Vignatavan - Limit definition of derivative
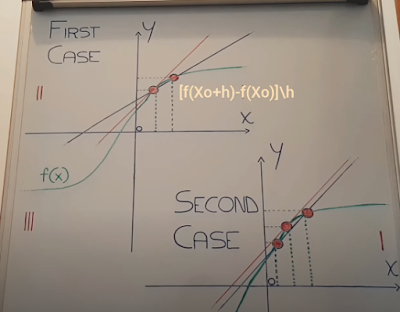
DERIVATIVES: the limit definition Nicolò Vignatavan -> Video According to traditional mathematics, the derivative of a function at one of its points "Xo" is infinitesimally equivalent to the incremental ratio [f(Xo + h) - f(Xo)] / h, with "h" meaning "Delta x", or in other words, the difference between the abscissa of the upper extremity, in direction x of the segment of dimension "h", constructed starting from "Xo" and the same lower extremity point "Xo" and "[f (Xo + h ) - f (Xo)] " is understood as " Delta y ", with " f (Xo + h) " and " f (Xo) considered respectively as the images on the axis of the ordinates of the two extreme points in denominator, with h tending to 0. In these terms, assuming a secant line to the function precisely at the ordinate points "f (Xo + h)" and "f (Xo)", considered as the i...