Nicolò Vignatavan - Limit definition of derivative

DERIVATIVES: the limit definition

Nicolò Vignatavan

-> Video

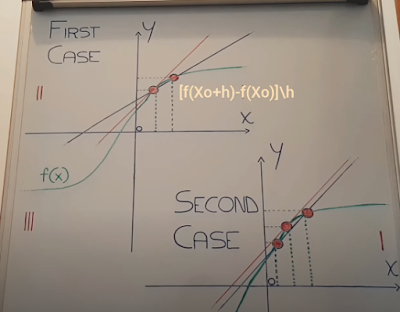
According to traditional mathematics, the derivative of a function at one of its points "Xo" is

infinitesimally equivalent to the incremental ratio [f(Xo + h) - f(Xo)] / h, with "h" meaning "Delta x", or

in other words,  the difference between the abscissa of the upper extremity, in direction x of the

segment of dimension "h", constructed starting from "Xo" and the same lower extremity point

"Xo" and "[f (Xo + h ) - f (Xo)] "  is understood as  " Delta y ", with " f (Xo + h) "  and " f (Xo)

considered respectively as the images on the axis of the ordinates of the two extreme points in

denominator, with h tending to 0.

In these terms, assuming a secant line to the function precisely at the ordinate points "f (Xo +

h)" and "f (Xo)", considered as the intersections of the same function with the extremes of the

closed and derivable interval "x" in which it is analyzed, in the instant in which h tends

infinitesimally to 0, the line becomes tangent to the function at the point "Xo". The slope of this

line, at the moment of tangency, is defined as the numerical value of the derivative at this point.

If h were equal to 0, the straight line would separate from the function, moving externally.  Now

let us assume that along the abscissa axis, instead of constructing towards segment "x", we

construct a segment "h" starting from point "Xo", and we set a circular neighborhood of point

"Xo" with a dimension of "2h", constructing by starting from the "Xo" point, along the x axis, 

a segment "h" in the -oo direction and another of the same length at the + oo direction. In this

way, the incremental ratio will result to be  [f (Xo + h) - f (Xo - h)] / 2h.

If in the first case the secant line, where h tends to 0,  becomes tangent to the "Xo" point by

rotating  itself, since one end is a fixed constraint and the other is mobile, in the second case, it

first presents itself as a circular neighborhood of the point "Xo", therefore, two equivalent "h"

distances along the x axis, the secant line becomes tangent not only by rotating  itself, but also

by varying ordinate, whose angular coefficient will be, at the end of the movement, that of the

line tangent to the point "Xo".

For this reason, in my opinion, this second approach is the most complete to define the concept

of a derivative.